Prognosemodelle
Allgemein
Die folgenden 11 Prognosemodelle stehen zur Verfgung:
- Manuelle Prognose (auf jhrlichem Bedarf basierend)
- Einfacher gleitender Durchschnitt
- Exponentielle Glttung mit Niveau
- Exponentielle Glttung mit Niveau und Trend
- Naive Prognose
- Adaptive exponentielle Glttung mit Niveau
- Regressionsgerade (kleinste Quadrate)
- Optimale Anpassung (whlt aus den 7 Prognosemodellen das beste fr eine bekannte historische Periode aus).
- Brownsche Glttung mit Niveau und Trend
- Crostons intermittierendes Modell
- Mehrfachregression
- Berechnungsmodell nach Bayes
- Lebenszyklus
- Regelbasiert
- ML-Wetter
Alle diese Prognosemodelle (mit Ausnahme des naiven Modells und der mehrfachen Regression) knnen mit periodischen Saisonindizes kombiniert werden. Die Multiplikation des errechneten Basiswerts der Prognose mit dem aktuellen Indexwert fr die gleiche Periode ergibt den Endwert der Prognose. Saisonindizes werden bei saisonbedingten Bedarfsschwankungen verwendet. Diese Indizes sind ausfhrlich unter Saisonindizes erklrt.
Einfhrung
Notation
| Y | Erwarteter Jahresbedarf. |
| N | Anzahl der Perioden pro Jahr. |
| Dt | Beobachteter Bedarf in Periode t |
| LT | Geschtztes Niveau in Periode t |
| TT | Geschtzter Trend in Periode t |
| Prognose in Periode t fr eine n Perioden in der Zukunft liegende Periode | |
| t=0 | Erste Periode mit historischem Bedarf. |
| t=h | Letzte Periode mit historischem Bedarf. |
| x | Anzahl der fr den einfachen gleitenden Durchschnitt verwendeten Perioden. |
| n | Anzahl der zu prognostizierenden Perioden. |
| a | Alpha: eine Glttungskonstante fr Niveau, |
| b | Beta: eine Glttungskonstante fr Trend, |
| r | Rho: ein Parameter zur Verringerung des langfristigen Trends, |
1. Manuelle Prognose
Dieses Modell liefert auf der Basis eines festen Jahresbedarfs den durchschnittlichen Bedarf pro Periode. Die Prognose, die in Periode t beginnt und fr zuknftige Perioden (t + n) gltig ist, wird durch die folgende Formel gegeben:
![]()
2. Einfacher gleitender Durchschnitt
Beim gleitenden Durchschnitt wird angenommen, dass in kurzem zeitlichen Abstand gemachte Beobachtungen mit hoher Wahrscheinlichkeit hnliche Werte aufweisen. Daher sollte der Durchschnitt mehrerer Zeitpunkte, die sich in der Nhe eines bestimmten Zeitpunktes befinden, einen brauchbaren Schtzwert fr den Trendzyklus whrend dieser Periode ergeben. Durch die Berechnung des Durchschnitts wird die Zufallsverteilung in den Daten reduziert und eine geglttete Trendzykluskomponente erzeugt. Das Prognosemodell besitzt keinen expliziten Trend, die Prognose entspricht daher fr jede zuknftige Periode dem Durchschnitt der letzten x Beobachtungsperioden.
Zur Beschreibung dieses Verfahrens wurde der Begriff "gleitender Durchschnitt" gewhlt, da jeder Durchschnittswert berechnet wird, indem die lteste Beobachtung durch die jngste Beobachtung ersetzt wird. Angenommen, es soll ein dreimonatiger gleitender Durchschnitt verwendet werden. Die Prognose wird fr Januar als Summe des Bedarfs im Oktober, November und Dezember, dividiert durch 3, berechnet. Bei der Berechnung der Februar-Prognose wird der Oktober-Bedarf durch den Januar-Bedarf ersetzt.
Die allgemeine Prognose auf der Grundlage des gleitenden Durchschnitts wird mit der folgenden Formel berechnet:
![]()
3. Exponentielle Glttung
Bei diesem Modell werden die historischen Daten unterschiedlich gewichtet. Die Gewichte nehmen typischerweise vom jngsten zum ltesten Datenpunkt exponentiell ab, d.h., das Modell berechnet einen gewichteten Durchschnitt von historischen Beobachtungen und verwendet dazu leicht sinkende Gewichte.
Der Gewichtungsparameter wird auch Glttungsparameter genannt. Wenn der Glttungsparameter auf 0,20 gesetzt wird, wird die letzte Periode mit 20%, die vorletzte Periode mit 16% (= 0,20 * (1 - 0,20)) und die vorvorletzte Periode mit 12,8% gewichtet. Dieser Vorgang wird fortgesetzt, bis die lteste Periode innerhalb der exponentiellen Berechnung erreicht wurde. Die Summe dieser Gewichte wird arithmetisch auf 1,0 korrigiert.
Wenn der Glttungsparameter auf den hchsten empfohlenen Wert 1,0 gesetzt wird, ist der vom Modell fr die nchste Periode prognostizierte Wert gleich dem Wert der jngsten Periode. Bei einem Glttungsparameter von 0,0 haben die zurckliegenden Perioden keinen Einfluss auf die Prognose, die ihr ursprngliches Niveau beibehlt.
Zur Berechnung des Anfangswerts der Prognose verwendete Formel
Der anfngliche Prognosewert ist der Schnittpunkt der Regressionslinie des historischen Bedarfs. Siehe L-1 in der Formel fr exponentielle Glttung, korrigierter Trend weiter unten.
Zur Berechnung aktueller Prognosen verwendete Formeln
Ausgehend von der ersten historischen Periode wird das Niveau mit der folgenden Formel aktualisiert:
![]()
Die in Periode t erstellte Prognose fr eine zuknftige Periode (t + n) ist durch folgende Formel gegeben:
![]()
4. Exponentielle Glttung mit Niveau und Trend
Wenn die Entwicklung des Bedarfs einem stetigen Trend folgt, bleiben Prognosen auf der Grundlage des gleitenden Durchschnitts oder der exponentiellen Glttung hinter dem aktuellen Bedarf zurck. Daher bedarf es einer weiteren Komponente, mit deren Hilfe dieses Zurckbleiben eliminiert wird. Neue Werte sollten signifikant hher oder tiefer als die vorherigen Werte sein. Der Trendzyklus T gibt einen Schtzwert fr die Steigung der Prognose an. Da es in den laufenden Bedarfsbeobachtungen noch eine gewisse Zuflligkeit geben kann, wird der Trend T durch Glttung mit einem Parameter b modifiziert.
Die Aktualisierungen von Niveau und Trend folgen dem gleichen Prinzip und verwenden die folgenden Formeln:
![]() ,
,
![]() .
.
Die Werte fr Schnittpunkt L-1 und Steigung T-1werden durch die folgenden Formeln initialisiert:
Schnittpunkt![]()
![]()
Steigung
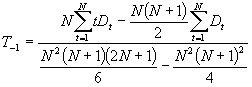
Die in Periode t berechnete Prognose fr eine zuknftige Periode (t + n) ist durch folgende Formel gegeben:
![]()
Es ist zu beachten, dass der Reduktionsfaktor R, der den Trendeffekt impliziert, reduziert wird. Langfristig nhert er sich an 0 an. r sollte nahe 1,0 festgelegt werden. Wenn r gleich 1,0 gewhlt wird, erfolgt keine Reduzierung des Trendeffekts.
5. Naive Prognose
Auch als ?Random Walk? bezeichnet. Diese Prognose verwendet nur den Umsatz der vorherigen Periode als Prognose fr diese Periode.
Zur Berechnung aktueller Prognosen verwendete Formeln
![]()
6. Adaptive exponentielle Glttung
Dieses Modell ist der exponentiellen Glttung sehr hnlich. Es wird auch ARRSES genannt: Adaptive Response Rate Single Exponential Smoothing (adaptive exponentielle Glttung der Reaktionsrate). Der Unterschied zwischen der normalen exponentiellen Glttung und diesem Modell besteht darin, dass es bei diesem Modell mglich ist, den Wert fr Alpha in kontrollierter Weise an nderungen in den Datenmustern anzupassen. Die Formeln dieses Modells sind gleich den Formeln der exponentiellen Glttung, auer dass der Wert von a (Alpha) durch a(t) ersetzt wird:
![]()
![]()
![]()
![]()
Zur Berechnung aktueller Prognosen verwendete Formeln
Ausgehend von der ersten historischen Periode wird das Niveau mit der folgenden Formel aktualisiert:
![]()
Die in Periode t erstellte Prognose fr eine zuknftige Periode (t + n) ist gegeben durch:
![]()
Startwerte sind:
L-1 entspricht der exponentiellen Glttung.
A-1 = B-1 = 0
Der Startwert fr Alpha fr die h/4 Perioden wird auf den Anfangswert gesetzt. Dann werden die Alpha-Werte allmhlich korrigiert. Wenn zum Beispiel ein Artikel 24 Perioden historischen Bedarfs aufweist, wird Alpha fr die 24/4 = 6 ersten Perioden des Bedarfs auf den Anfangswert gesetzt.
7. Regression
Dieses Prognosemodell ist eine lineare Anpassung der historischen Perioden entsprechend der Methode der kleinsten Quadrate.
Regressionsgerade
![]()
Schnittpunkt![]()
![]()
Steigung
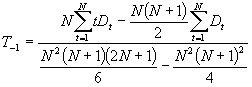
Zur Berechnung aktueller Prognosen verwendete Formeln
![]()
8. Brownsche Glttung mit Niveau und Trend
Dieses Modell ist dem oben erwhnten Modell Exponentielle Glttung, korrigierter Trend sehr hnlich. Der einzige Unterschied besteht darin, dass aund b in der Prognosegleichung durch ab und bb ersetzt werden. Sie geben nur einen Parameter a ein, der gem den folgenden Gleichungen verwendet wird.
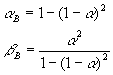
Ein Sonderfall ist, wenn a auf 0 gesetzt wird, dann ist a b=0 und b b=0.
Zur Berechnung aktueller Prognosen verwendete Formeln
Niveau und Trend werden mit den folgenden Formeln aktualisiert:
![]()
![]()
Die Prognose, die in Zukunft fr eine zuknftige Periode (t+n) erstellt wird, ist gegeben durch:
![]()
Hinweis: Der Verkleinerungsfaktor r, der den Trendeffekt beeinflusst, wird reduziert; langfristig nhert er sich an 0 an. r sollte nahe 1,0 festgelegt werden. Wenn r gleich 1,0 gewhlt wird, erfolgt keine Reduzierung des Trendeffekts.
Startwerte sind:
Die Werte fr L -1 und Steigung T-1 entsprechen denjenigen des Modells Exponentielle Glttung, korrigierter Trend (siehe oben).
9. Optimale Gre
Bei diesem Prognosemodell werden alle Modelle ausgefhrt, die fr den letzten bekannten historischen Bedarf Werte liefern. Das Modell mit dem besten Ergebnis wird als Prognosemodell fr diesen Artikel ausgewhlt. Sie knnen auswhlen, welche Fehlermae die Basis fr die Mitbewerber werden sollen. Sie knnen auswhlen, ob Sie den Parameter MAE oder MSE optimieren wollen. Siehe Erweiterte Servereinstellungen definieren zu Auswahl der optimierten Messung. Die Prognosemodelle werden mit verschiedenen Parametern ausgefhrt, so dass auch die Parameter optimiert werden.
Bei der Suche nach den optimalen Parametern wird eine lineare Schrittgre verwendet. Bei einer Schrittgre von 0,025 funktioniert der Optimierungsalgorithmus wie folgt: Beginnend mit Parameter1 = 0, dann wird Parameter 2 in 0,025-Schritten von 0 auf 1 erhht. Anschlieend Parameter1 um 0,05 erhhen, und einen weiteren Lauf mit Parameter2 durchfhren. Ist nur ein Parameter vorhanden, wird nur ein Lauf ausgefhrt. Die Schrittgre wird durch den Eintrag BestFitNoOfAlphaSteps oder BestFitNoOBetaSteps der erweiterten Servereinstellungen festgelegt (siehe unten). Das Modell "Gleitender Durchschnitt" wird mit allen mglichen Lngen fr die Anzahl der Perioden (2..n) ausgefhrt.
Bei der Auswahl des optimalen Modells werden die folgenden Prognosemodelle ausgefhrt:
- Manuelle Prognose (auf jhrlichem Bedarf basierend)
- Einfacher gleitender Durchschnitt
- Exponentielle Glttung mit Niveau
- Exponentielle Glttung mit Niveau und Trend
- Naive Prognose
- Adaptive exponentielle Glttung mit Niveau
- Regressionsgerade (kleinste Quadrate)
- Brownsche Glttung mit Niveau und Trend
Jedes Prognosemodell wird ausgefhrt, wobei die Parameter folgendermaen ausgewhlt werden:
Gleitender Durchschnitt
Es werden alle mglichen Varianten fr die Anzahl der Perioden von min_average_period_number bis n getestet. N = Anzahl der historischen Perioden fr diesen Artikel. Der Standardwert fr die Mindestanzahl der Perioden fr die Durchschnittsberechnung ist 1.
- Mindestanzahl der Perioden fr die Durchschnittsberechnung: ForecastModels/BestFitMovingAverageMinPeriods
Kleinste Quadrate-Methode
Keine einstellbaren Parameter.
EWMA (Niveau)
Der Alpha-Wert wird hierbei in 25 Schritten zwischen 0,01 und 0,3 gendert (Standard). Die Grenzwerte knnen in den folgenden Eintrgen der erweiterten Servereinstellungen gendert werden:
- Unterer Alpha-Grenzwert ForecastModels\BestFit\EWMA_AlpaStart
- Oberer Alpha-Grenzwert ForecastModels\BestFit\EWMA_AlpaStop
- Anzahl der Alpha-Schritte ForecastModels\BestFit\NoOfAlphaSteps
EWMA (Niveau/Trend)
Der Alpha-Wert wird hierbei in 25 Schritten zwischen 0,02 und 0,51 gendert. Beta wird zwischen 0,005 und 0,18 in 25 Schritten gendert (Standard). Die Grenzwerte knnen in den folgenden Eintrgen der erweiterten Servereinstellungen gendert werden:
- Unterer Alpha-Grenzwert ForecastModels\BestFit\EWMATREND_AlpaStart
- Oberer Alpha-Grenzwert ForecastModels\BestFit\EWMATREND_AlpaStop
- Unterer Beta-Grenzwert ForecastModels\BestFit\EWMATREND_BetaStart
- Oberer Beta-Grenzwert ForecastModels\BestFit\EWMATREND_BetaStop
- Anzahl der Alpha-Schritte ForecastModels\BestFit\NoOfAlphaSteps
- Anzahl der Beta-Schritte ForecastModels\BestFit\NoOfAlphaSteps
AEWMA
Hierbei wird der Startwert von Alpha auf 0,2 gesetzt. Die Beta-Werte werden in 25 Schritten zwischen 0,1 and 0,3 gendert (Standard). Die Grenzwerte knnen in den folgenden Eintrgen der erweiterten Servereinstellungen gendert werden:
- Unterer Beta-Grenzwert ForecastModels\BestFit\AEWMA_BetaStart
- Oberer Beta-Grenzwert ForecastModels\BestFit\AEWMA_BetaStop
- Anzahl der Beta-Schritte ForecastModels\BestFit\NoOfAlphaSteps
Es ist zu beachten, dass es in den erweiterten Servereinstellungen gemeinsame Variablen gibt, die die Anzahl der Schritte fr die Alpha- und Beta-Parametersuche festlegen.
Die Rho-Verkleinerung wird nicht gendert. Wenn ein Prognosemodell mit einem Saisonprofil verknpft ist, wird das Saisonprofil bei der Ausfhrung des Optimierungsalgorithmus auf alle Berechnungen angewendet.
Niveau und Trend nach Brown
Hierbei werden die Alpha-Werte in 25 Schritten zwischen 0,01 und 0,3 gendert (Standard). Die Grenzwerte knnen in den folgenden Eintrgen der erweiterten Servereinstellungen gendert werden:
- Unterer Alpha-Grenzwert ForecastModels\BestFit\Brown_AlpaStart
- Oberer Alpha-Grenzwert ForecastModels\BestFit\Brown_AlpaStop
- Anzahl der Alpha-Schritte ForecastModels\BestFit\NoOfAlphaSteps
10. Crostons intermittierendes Modell
Dieses Prognosemodell ist ein speziell fr Artikel mit sporadischem Bedarf (schwer verkufliche Artikel) zu verwendendes Modell. Es berechnet die Hufigkeit des Bedarfs und die Bedarfshhe getrennt voneinander.
Definitionen
| n | Seriennummer einer Periode mit tatschlichem Bedarf ungleich 0. |
| n' | Zur Initialisierung verwendete verknpfte Seriennummer fr Bedarf ungleich 0. |
|
|
Erwartete Hhe des Bedarfs. |
|
|
Erwartetes Intervall zwischen zwei Bedarfsfllen. |
|
|
Tatschliches Intervall zwischen zwei Bedarfsfllen. |
Installation
Im ursprnglichen Algorithmus ist fr die Initialisierung des Modells eine recht groe Menge von Daten erforderlich. In vielen Fllen liegt diese Datenmenge aufgrund der sporadischen Natur des Bedarfs nicht vor. Hier wird eine Erweiterung des ursprnglichen Algorithmus vorgestellt, die auf einem Verfahren zur Bildung einer empirischen Verteilung beruht. Zur Initialisierung des Modells sind 5 historische Bedarfsflle erforderlich. Zunchst mssen diese 5 historischen Bedarfsflle auf 25 Vorkommnisse erweitert werden, indem 5 Wiederholungen der vorhandenen Serie aneinandergeknpft werden. Dann werden die folgenden Gleichungen angewendet.
![]()
![]()
Rekursive Aktualisierung
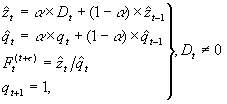
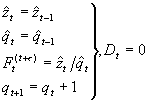
Die in Periode t erstellte Prognose fr eine zuknftige Periode (t + n) ist gegeben durch:
![]()
Hinweis zu Fehlermessgren und der Croston-Methode
Die normalen Mae MAE, MAE-Wert, MSE und ME lassen sich anwenden, da sie die Prognose, die fr alle Perioden einen Erwartungswert darstellt, mit dem tatschlichen Bedarf vergleichen und damit korrekt ist.
Wenn der tatschliche Bedarf gleich 0 ist, fhrt MAPE, WMAPE und RME zur Division durch 0 und kann daher nur bei Perioden mit einem Bedarf ungleich 0 aktualisiert werden. Dieses Ma ist daher fr Artikel mit intermittierendem Bedarf irrelevant.
PVE und Verfolgungssignal lassen sich fr Artikel mit intermittierendem Bedarf nicht sinnvoll interpretieren. Daher sollte der Anwender darauf verzichten, sie einzusetzen.
Das Konfidenzintervall ist relativ gro, da es um den prognostizierten Wert liegt und auf der Messgre MAE basiert. Es ist nicht sinnvoll, es zum Erkennen von Ausreiern zu verwenden, aber es vermittelt eine Vorstellung von der Schwankung des mittleren Bedarfs fr alle Perioden.
Hinweis zu Croston und Prognoseanpassungen
Wenn Sie das Crostonsche Prognosemodell verwenden und die Prognose anpassen wollen, mssen Sie den erwarteten Bedarf in der Detailansicht nach oben oder unten ndern, sodass die Formel Erwartete Bedarfsgre= durchschnittliche angepasste Prognose* Intervall zwischen Bedarfen gltig ist. Der Anwender kann auch das Feld ?Intervall zwischen Bedarfen? in der Detailansicht anpassen. Dies ndert wiederum die erwartete Bedarfsgre, sodass die obige Gleichung gltig ist. Das Feld Sys. Erwartete Bedarfsgre und Sys. Das Intervall zwischen den Bedarfen in der Detailansicht ist das Ergebnis der obigen Berechnung.
11. Mehrfachregression
Bei der mehrfachen Regression wird eine vorherzusagende Variable (z.B. Verkauf) auf der Grundlage von zwei oder mehr Erklrungsvariablen vorhergesagt. (Die allgemeine mathematische Formel folgt weiter unten.) Ist also etwa der Verkauf die vorherzusagende Variable, knnen mehrere Faktoren wie beispielsweise das Bruttosozialprodukt, Reklame, Preise, Konkurrenz und Zeit den Verkauf beeinflussen. Alle oder ein Teil dieser Variablen knnen zur Berechnung der Verkaufsprognose dieses Produkts verwendet werden. Erklrungsvariablen knnen auch zur Erklrung der zeitabhngigen Auswirkungen auf den Umsatz wie saisonale nderungen, Schwankungen an Handelstagen, variable Auswirkungen von Feiertagen etc. verwendet werden. So knnen beispielsweise saisonale nderungen betrachtet und vierteljhrliche Periodenversionen zum Hinzufgen von Erklrungsvariablen fr saisonale nderungen angenommen werden. Es werden drei Erklrungsvariablen mit den folgenden Werten hinzugefgt:
| Quartal | Erklvar 1 | Expvar 2 | Expvar 3 |
| 1. Quartal | 0 | 0 | 0 |
| 2. Quartal | 1 | 0 | 0 |
| 3. Quartal | 0 | 1 | 0 |
| 4. Quartal | 0 | 0 | 1 |
Mehrfachregression - Modell
Die Regression beginnt in der ersten Periode, in der fr alle Erklrungsvariablen und fr den historischen Bedarf des Artikels Daten vorliegen. Falls fr eine Erklrungsvariable in keiner Prognoseperiode Daten vorliegen, wird die letzte Periode in die fehlenden Perioden kopiert.
![]()
Wobei Yi, X1i, ..., Xk die i-ten Betrachtungen der Variablen Y, Xi, ..., Xi (Y ist der Artikelverbrauch, die X sind die Erklrungsvariablen) sind, b0, b1,..., bk sind feste aber unbekannte Parameter, und ei ist der geschtzte Fehler.
Die Regressionskoeffizienten auflsen
![]()
![]()
Die Methode der kleinsten Quadrate wird verwendet, um die kleinste Summe der Fehlerquadrate zu ermitteln und so den Ausdruck b0 ,b1,...,bk zu minimieren.
![]()
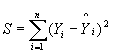
![]()
Partielle Abweichungen von S in Bezug auf einzelne der unbekannten Koeffizienten b0 ,b1,..., bk ,diese Abweichungen auf 0 (null) setzen und eine Reihe von k Gleichungen mit k Unbekannten lsen, um die geschtzten Werte zu erhalten b0 ,b1,..., bk.
![]()
![]()
![]()
.....
Der Gleichungssatz AX=B wird durch Gausche Eliminierung gelst.
Die in Periode t erstellte Prognose fr eine zuknftige Periode (t+ n) ist gegeben durch:
![]()
12. Berechnungsmodell nach Bayes
Diese Prognose stellt 1/4 der 4 anderen Prognosemodelle dar. Die 4 verwendeten Modelle sind:
- Gleitender Durchschnitt
- Adaptive EWMA
- Regression (kleinste Quadrate)
- Brownsche Glttung mit Niveau und Trend
Um die Parameter fr die verschiedenen Modelle zu finden, wird eine Suche nach dem Parameter fr die optimale Anpassung ausgefhrt, siehe Optimale Anpassung. Dies bedeutet, dass wir den "optimalen" Parametersatz fr jedes der 4 Modelle finden. Dann besteht dieses Modell aus 1/4 jedes der 4 Modelle.
Beachten Sie, dass Sie auch feste Parameter fr die verschiedenen Modelle im Bayes?schen Prognosemodell verwenden knnen. Siehe Erweiterte Servereinstellungen.
Zur Berechnung aktueller Prognosen verwendete Formeln
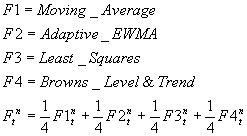
Im Eintrag ForecastModels\Bayesian\BayesianInitPeriods der erweiterten Servereinstellungen knnen Sie definieren, fr wie viele Perioden der Artikel Historien haben muss, bevor das Bayes-Modell angewendet werden kann. Wenn das Bayes?sche Modell ausgewhlt wird und der Artikel nicht genug historische Werte aufweist, wird der gleitende Durchschnitt (ber alle Perioden) als Prognosemodell verwendet. Beachten Sie, dass der Artikel noch nach dem Bayes?schen Prognosemodell behandelt wird. Normal Bayes wird zur Erstellung der Prognose verwendet, sobald der Artikel den Grenzwert erreicht. Standardwert ist 4. Siehe Erweiterte Servereinstellungen definieren.
13. Lebenszyklus
Dieses Prognosemodell besteht aus 2 separaten Formeln. Eine zur Berechnung der Phase ?Gltig ab? und eine zur Berechnung der Phase ?Gltig bis?.
Gltig ab:
Unter den Parametern fr die Phase ?Gltig ab? befindet sich die Sttigungsstufe. Sie bezeichnet das erwartete Niveau der Umstze beim Erreichen der Flligkeit, die Startstufe ist der erwartete Absatz in der ersten Periode, die Startperiode und die Endperiode (Periodenlnge der Phase) der Phase ?Gltig ab?.
<![if!msEquation]>
<![if !vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if !vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if !vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if !vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if !vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if !vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if !vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if!vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if!vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if!vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
Dann wird die Prognose angegeben von:
<![if!msEquation]>
<![if !vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if !msEquation]>Gltig bis:<![endif]>
<![if !msEquation]><![endif]>Unter den Parametern fr ?Gltig bis? befindet sich die Sttigungsstufe. Sie bezeichnet das erwartete Niveau der Umstze beim Erreichen der Flligkeit und die Lnge der Periode ?Gltig bis?.<![if !msEquation]><![endif]>
<![if !msEquation]><![if!vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if!vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if!vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
Dann wird die Prognose angegeben von:
<![if!msEquation]>
<![if!vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if !msEquation]>Saturation Update<![endif]>
<![if !msEquation]>Whrend der Phasen ?Gltig ab? und der Phase ?Gltig bis? wird die Sttigungsstufe abhngig davon, ob der tatschliche Absatz ber oder unter den prognostizierten Werten liegt, angepasst. Wenn der tatschliche Absatz unter diesem Wert liegt, wird die Sttigungsstufe gesenkt; wenn er darber liegt, wird die Sttigungsstufe erhht. Dies geschieht durch die exponentielle Glttung mit der Alfa-Glttungskonstante.<![endif]>
<![if !msEquation]>Dies wird mit der folgenden Formel bestimmt:<![endif]>
<![if !msEquation]><![if!vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]>
<![if!vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if !vml]>![]() <![endif]>
<![endif]>
<![if!msEquation]>
<![if!vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
<![if!msEquation]> <![if !vml]>![]() <![endif]><![endif]>
<![endif]><![endif]>
14. Regelbasiert
Dieses Modell kann basierend auf der Anzahl der verfgbaren historischen Datenperioden automatisch verschiedene Prognosemodelle anwenden, z.B. ?Manuell?, ?Gleitender Durchschnitt? und ?Bayes? fr Prognoseartikel/-gruppe/-abfrage.
Im Eintrag ForecastModels\RuleBased\Period_Start_Moving _Average der erweiterten Servereinstellungen knnen Sie definieren, wie viele historische Datenperioden der Artikel haben muss, bevor das gleitende Durchschnittsmodell verwendet wird. Der Standardwert ist 3. Wenn das regelbasierte Modell ausgewhlt wird und der Artikel nicht genug historische Werte aufweist, wird das manuelle Modell als Prognosemodell verwendet. Hinweis: In der Detailansicht des Prognoseartikels wird weiterhin ?Regelbasiert? als Standardprognosemodell und ?Manuell? als Prognosemodell verwendet.
Im Eintrag ForecastModels\RuleBased\Period_Start_Bayesian der erweiterten Servereinstellungen knnen Sie definieren, wie viele historische Datenperioden der Artikel haben muss, bevor das gleitende Bayes-Modell verwendet wird. Der Standartwert ist 6. Wenn das regelbasierte Modell ausgewhlt wird und der Artikel nicht genug historische Werte aufweist, wird das gleitende Durchschnittsmodell oder das manuelle Modell als Prognosemodell verwendet. Hinweis: In der Detailansicht des Prognoseartikels wird weiterhin ?Regelbasiert? als Standardprognosemodell und ?Gleitender Durchschnitt? oder ?Manuell? als Prognosemodell verwendet. Wenn die Anzahl verfgbarer historischer Datenperioden mehr als 6 betrgt, wird Bayes als Prognosemodell angezeigt. Unter Erweiterte Servereinstellungen definieren finden Sie ausfhrliche Informationen zur Auswahl von Eintragswerten fr erweiterte Servereinstellungen.
15. ML-Wetter
Bei diesem Prognosemodell handelt es sich um ein Kurzzeitmodell (1 bis 14Tage), das ein Zeitreihenvorhersagemodell auf der Grundlage von Wetterdaten bietet. Es verwendet nichtlineare Regression mit hoher Flexibilitt zur Anpassung an beliebige Daten ohne Vorannahmen ber die tatschlichen Datenmuster. Das Modell nutzt einen externen Wetterdienstleister, um historische Wetterdaten zu sammeln. Diese Daten werden zusammen mit den historischen Artikeldaten zum Trainieren des Modells und der Wetterprognosebedingungen verwendet, um den Bedarf oder die Prognose 14Tage im Voraus vorherzusagen bzw. zu erstellen. Wie bei den meisten Prognosemodellen wird das Ergebnis besser, je mehr historische Daten vorhanden sind. Das Modell sucht nach Korrelationen zwischen den Verkufen/Verbruchen und den verschiedenen Wetterparametern. Die knftige Prognose ist das Ergebnis der gefundenen Korrelationen und der Wettervorhersage fr die nchsten 14Tage. Das Vorhersagemodell nach Bayes wird zur Berechnung der Vorhersage verwendet, die die ersten 14Tage auf die letzte Vorhersageperiode erweitert, sodass Artikel, die dieses Modell verwenden, immer noch die gleiche Vorhersageperiode wie die anderen Modelle haben.
Jedes Modell reprsentiert einen bestimmten Artikel, wobei die Wetterdaten auf einem geografischen Ort basieren, an dem der Artikel verwendet/verbraucht wird. Dieser Ort ist mit dem Basis-Flow in der Bedarfsplanung verbunden.
Die Wetterdaten enthalten die folgenden Merkmale:
1. Durchschnittliche Temperatur
2. Min. Temperatur
3. Max. Temperatur
4. Gesamtniederschlag
5. Windgeschwindigkeit
6. Luftfeuchtigkeit
7. Schneefall insgesamt
8. Visibility
9. Windben
10. Bewlkung
11. Windrichtung
Hinweis: Damit dieses Modell funktioniert, muss das maschinelle Lernen auf dem Bedarfsplanungs-Server aktiviert sein und alle erforderlichen Einstellungen mssen vorhanden sein
- Einrichtung der Machine Learning Engine
- Muss mit den Ausfhrungszeiten des Bedarfsplanungsauftrags synchronisiert werden (nach Abschluss des Jobs ?Tglich zusammenfassen?)
- Einrichtung des Bedarfsplanungs-Servers
- Bedarfsplanungs-Server, maschinelles Lernen aktivieren
- Basis-Flows, Standortdetails
- Job ?Tglich zusammenfassen?, Planung fr tgliche Ausfhrung
- Die Artikel mssen eine Historie von mindestens 180Tagen haben.
Es gibt auch eine Vorlaufzeit, bevor Sie die berechneten Ergebnisse erhalten. Diese Vorlaufzeit betrgt maximal 7Tage. Der Grund dafr ist, dass dieses Modell ein Training der Algorithmen erfordert und dieses Training nur einmal pro Woche durchgefhrt wird. Artikel mit weniger als 180Tagen an historischen Daten werden nicht trainiert/berechnet.